Lineární lomená funkce

Vydáno dne 9. 2. 2011 v kategorii Funkce; Autor: Jakub Vojáček; Počet přečtení: 212 037

Úvod do problematiky lineární lomené funkce - definiční obor, náčrtek grafu a řešené příklady

Lineární lomená funkce je funkce ve tvaru $f(x)=\frac{a\mathrm{x}+b}{c\mathrm{x}+d},a, b,c, c \in \mathbb{R}, c \neq 0$

Graf funkce $f(x)=\frac{1}{x}$

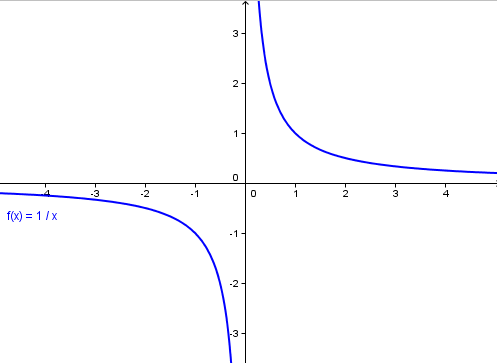
Grafem lineární lomené funkce je hyperbola a její předpis už jste viděli. Je zde ale jedna maličkost, na kterou si musíte dát pozor. Rovná-li se totiž ad-bc=0 , pak je grafem funkce přímka s předpisem $f(x)=\frac{a}{c}$ .

Vlastnosti lineární lomené funkce

Definičním oborem (Definiční obor) jsou všechna reálná čísla až na jedno. Ve jmenovateli totiž nesmí být nula a proto víme, že $c\mathrm{x} +d \neq 0$ . Upravením této nerovnice dojdeme k výsledku, že definičním oborem funkce je: $D_f = \mathbb{R}\backslash\left\{-\frac{d}{c}\right\}$
Oborem hodnot je $H_f = \mathbb{R}\backslash\left\{-\frac{a}{c}\right\}$
Funkce není omezená a nemá maximum ani minimum (Vlastnosti funkcí).
Pro se jedná o funkci rostoucí na celém svém definičním oboru.
Pro se jedná o funkci klesající na celém svém definičním oboru.
Funkce má dvě asymptoty (Asymptota funkce): $x=-\frac{d}{c},y=\frac{a}{c}$

Náčrtek grafu

Když dostanete za úkol načrtnout graf nějaké funkce, můžete spočítat její průběh, ale to je dlouhá a často obtížná cesta. Pokud ale poznáte, že se jedná o funkce lineárně lomenou, existuje pomůcka, jak její graf načrtnout. Pokud totiž dostaneme funkci do tvaru $f(x)=\frac{a}{x+m}+n;a,m,m\in\mathbb{R}$ , tak její graf bez problémů načrtneme.

Převod lineární lomené funkce do předchozího tvaru je jednoduchý - stačí funkci vydělit jako dva mnohočleny:

Ovšem pamatovat si takovýto vzorec je asi zbytečné, lehčí je vždy mnohočleny vydělit.

Převeďte funkci $f(x)=\frac{x+2}{x+4}$ na druhý tvar:


Platí tedy:

Převádět tedy umíte. Nyní k samotnému náčrtu grafu podle předpisu $f(x)=\frac{a}{x+m}+n;a,m,m\in\mathbb{R}$ :

Je-li , pak funkce je rostoucí. Je-li , funkce je klesající. Parametry , určují posun po ose x, y. Posunuje o ve směru kladné poloosy x a o ve směru kladné poloosy y.

Pro funkci $f(x)=\frac{1}{x+2}+1$ to vypadá následovně:

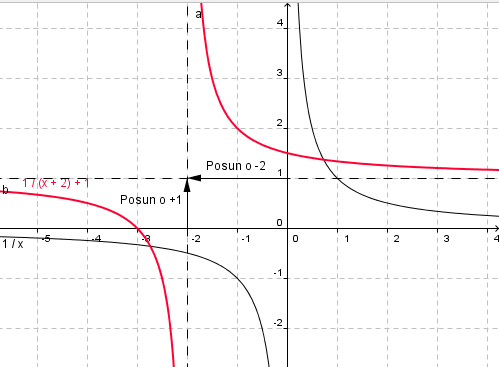
Vyzkoušíme si to ještě jednou. Určete definiční obor a obor hodnot funkce $f(x)=\frac{x-2}{x+2}$

Definiční obor a obor hodnot získáme pouhým dosazením do vzorečku.

`D_f = \mathbb{R}\backslash\left\{-\frac{d}{c}\right\}=\mathbb{R}\backslash\left\{-2\right\}`
$H_f = \mathbb{R}\backslash\left\{-\frac{a}{c}\right\}=\mathbb{R}\backslash\left\{1\right\}$

Abychom mohli načrtnout graf, musíme funkci upravit:

Z tohoto tvaru již graf načrtnete jistě snadno:

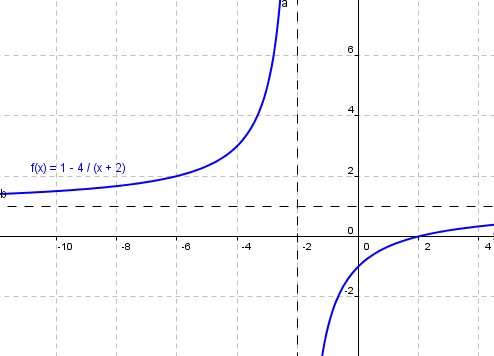
Lineární lomená funkce - příklady

Příklad 1: Výpočet definičního oboru

Mějme funkci `f(x) = \frac{2x + 1}{x - 3}`.

Definiční obor: Definiční obor této funkce je množina všech reálných čísel, kromě těch, kde je jmenovatel roven nule.

Jmenovatel je `x - 3`, takže roven nule bude, když `x = 3`.

Proto definiční obor `D_f` je: `D_f = \mathbb{R} \setminus \{ 3 \}`

Příklad 2: Výpočet oboru hodnot oboru

Mějme funkci `f(x) = \frac{4}{x + 2}`.

Hodnotový obor: Funkce není definována pro `x = -2`, což ovlivňuje definiční obor. Hodnotový obor zjistíme pomocí algebraické manipulace a analýzy limit.

Proto hodnotový obor `H_f` je: `H_f = \mathbb{R} \setminus \{ 0 \}`

Příklad 3: Výpočet definičního a oboru hodnot

Mějme funkci `f(x) = \frac{x + 1}{2x - 5}`.

Definiční obor: Jmenovatel nesmí být nulový, tj. `2x - 5 = 0`.

Řešením je `x = \frac{5}{2}`, což znamená, že funkce není definována pro toto a proto tedy `D_f = \mathbb{R} \setminus \left\{ \frac{5}{2} \right\}`

Obor hodnot: Funkce nemůže nabývat hodnoty, pro kterou by čitatel byl nulový, což pro tuto funkci není žádný další případ. Proto tedy `H_f = \mathbb{R}`.

Příklad 4: Asymptoty funkce

Uvažujme funkci `f(x) = \frac{3x - 2}{x + 1}`.

Svislá asymptota: Funkce má svislou asymptotu v bodě, kde je jmenovatel roven nule. To nastane pro `x = -1`.

Vodorovná asymptota: Pokud prozkoumáme chování funkce, když jde k nekonečnu, zjistíme, že vodorovná asymptota je `y = 3`, protože podíl `\frac{3x}{x}` jde k 3.

Asymptoty tedy jsou:
Svislá asymptota: `x = -1`
Vodorovná asymptota: `y = 3`

Příklad 5: Přímka rovnoběžná s asymptotou

Najděme přímku rovnoběžnou s asymptotou funkce `f(x) = \frac{5x - 4}{x - 2}` a procházející bodem `(0, -1)`.

Vodorovná asymptota je `y = 5`, takže přímka bude mít tvar `y = 5`. Aby však procházela bodem `(0, -1)`, posuneme ji dolů o 6 jednotek: `y = -1`.

Přímka rovnoběžná s asymptotou je tedy `y = -1`.

Příklad 6: Průsečík s osami

Mějme funkci `f(x) = \frac{2x + 3}{x - 4}`.

Průsečík s osou x: Nastavíme `y = 0` a řešíme rovnici `0 = \frac{2x + 3}{x - 4}`. To vede k rovnici `2x + 3 = 0`, což dává `x = -\frac{3}{2}`.

Průsečík s osou y: Nastavíme `x = 0` a dostaneme `f(0) = \frac{2(0) + 3}{0 - 4} = -\frac{3}{4}`.

Průsečíky jsou tedy:
S osou x: `\left(-\frac{3}{2}, 0\right)`
S osou y: `\left(0, -\frac{3}{4}\right)`

Příklad 7: Inverzní funkce

Uvažujme funkci `f(x) = \frac{x + 2}{x - 1}`.

Inverzní funkce: Nejprve nastavíme `y = f(x)`, tedy `y = \frac{x + 2}{x - 1}`. Řešíme tuto rovnici pro :

`y(x - 1) = x + 2`

`yx - y = x + 2`

`yx - x = y + 2`

`x(y - 1) = y + 2`

`x = \frac{y + 2}{y - 1}`

Inverzní funkce je tedy `f^{-1}(x) = \frac{x + 2}{x - 1}`.