Stereometrie se zabývá útvary, které nelze umístit do roviny. Mezi tyto útvary patří například hranol, krychle, kužel, jehlan a další. Slovo stereometrie je řeckého původu a jeho volný překlad je měření těles.
V planimetrii leží všechny útvary v jedné rovině. Těchto rovin může být ve stereometrii nekonečně mnoho. Mezi základní geometrické útvary patří přímka, bod a rovina.
Volné rovnoběžné promítání
Než se pustíme do složitějších úloh jako vzájemná poloha rovin či řezy krychlí, měli bychom se naučit promítnout 3D tělese do jedné roviny.
Krychle
Na tomto promítání není v zásadě nic těžkého. Nejdříve si musíme určit průmětnu. Útvary v této rovině (nebo rovnoběžné s touto rovinou) se zobrazují ve skutečné velikosti a ve skutečných úhlech. Útvary kolmé na průmětnu se promítají pod úhlem 45° a poloviční délkou. Každý z vás jistě již viděl krychli zobrazenou ve volném rovnoběžném promítání:

My si teď zkusíme trochu objasnit postup rýsování této krychle (o straně a=4cm). Nejprve narýsujeme čtverec (přední stranu) ABEF, jehož strany budou mít nezmenšenou velikost:

Pak musíme narýsovat úsečky vedoucí k zadní straně (DCHG). Tyto úsečky jsou kolmé na průmětnu a proto je zobrazíme pod úhlem 45° a délkou 2cm.

Nyní, když spojíme body DCHG, vznikla nám krychle ABCDEFGH!

Jehlan
Mezi narýsováním krychle a jehlanu zas takový rozdíl není, používají se stále stejné principy, přesto si postup raději krok po kroku vysvětlíme. Narýsujeme pravidelný čtyřboký jehlan ABCDV.
Začneme podstavou. Ta má tvar čtverce, proto budeme opět postupovat podobně jako při rýsování krychle:

Nyní musíme najít patu výšky. Ta se v jehlanu nachází na průsečíku úhlopříček dolní podstavy:

Spojíme li nyní bod V s body podstavy máme hotový jehlan ABCDV:

Pravidelný šestiboký jehlan
Další těleso, které zkusíme narýsovat bude pravidelný šestiboký jehlan. Toto těleso má jako podstavu pravidelný šestiúhelník. Ten musíme narýsovat jako první, zatím bez volného rovnoběžného promítání.

Nyní, když jsem si připravili podstavu, můžeme ji zkusit převést do volného rovnoběžného promítání. Přední hrana, tedy hrana AB je rovnoběžná s průmětnou a proto ji narýsujeme v původní velikosti. Úsečky AE a BD jsou v původním obrázku kolmé na AB a proto je nyní narýsujeme pod úhlem 45° a v poloviční velikosti. V šestiúhelníku prochází úsečka FC středy úseček AE a BD a tak tomu bude i ve volném rovnoběžném promítání. Navíc délka úsečka FC se nezmění, protože je rovnoběžná s průmětnou. Nyní stačí dokončit hrany spojením EF, AF, BC a DC. Pravidelný šestiúhelník ve volném rovnoběžném promítání je hotov.

Výška vychází z průsečíku úhlopříček a její velikost není zmenšena, protože výška je rovnoběžná s průmětnou. Pak stačí spojit jednotlivé body s vrcholem a máte pravidelný šestiboký jehlan.

Pravidelný trojboký jehlan
Podstavu pravidelného trojbokého hranolu tvoří rovnostranný trojúhelník. Výška jehlanu vychází z průsečíku těžnic.

Pokud by byla délka strany a = 3 cm, tak výška bude mít délku v≈=2.6. Jelikož je výška kolmá na průmětnu, tak ji zobrazíme pod úhlem 45° a s poloviční délkou.

Výška jehlanu opět vyhází z průsečíků těžnic:

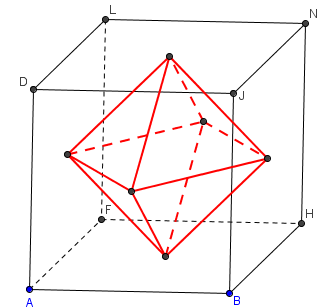
Osmistěn
A takto by vypadal například pravidelný osmistěn vepsaný do krychle:
Pro dnešek by to stačilo. V dalším díle si vysvětlíme základní vztahy mezi bodem, přímkou a rovinou.