Osová souměrnost je vlastně zobrazení nějakého bodu podle osy. Původní bod má od osy stejnou vzdálenost jako jeho odraz. Oba tyto body leží na přímce, která je kolmá na osu.
Při operaci osové souměrnosti zachováváme velikosti úhlů a délky úseček. Proto se jedná o shodné zobrazení.
V prvním odstavci jsem se pokusil slovně vysvětlit osovou souměrnost. Může to vypadat celkem složitě, ale opravdu tomu tak není. Snad to pochopíte na následujícím příkladu: Najděte bod A', který bude osově souměrný k bodu A podle osy o.

Začneme tedy tím, že uděláme kolmici k ose o, která by procházela bodem A.

Nyní stačí udělat bod A' ve stejné vzdálenosti od osy o jako je bod A. Pokud to rýsujete, použijte kružítko (zapíchněte ho do průsečíku osy a kolmice a udělejte kružnici procházející bodem A).

Pokud označíme průsečík osy o a kolmice q jako S, tak musí platit |AS| = |A'S|. Vidíte, není to nic těžkého:-)
V podstatě již umíte osovou souměrnost, ale pro jistotu zde uvedu několik dalších příkladů. Zobrazte trojúhelník ABC osově souměrný podle osy o.

Nejedná se o nic jiného než to, co jsme řešili v předchozím příkladě. Akorát máme teď tři body, které musíme osově zobrazit. Budeme tedy postupovat stejně jako před chvíli, tj. uděláme kolmice k ose o procházející postupně body A, B, C.
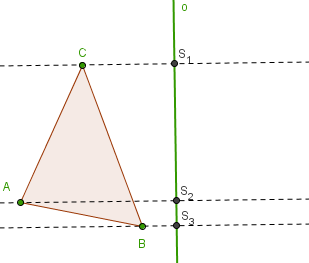
Abychom dokončili příklad stačí najít body A', B', C', aby platilo |CS1| = |C'S1|, |AS2| = |A'S2|, |BS3| = |B'S3|. K tomu použijeme opět kružítko.

Příklad je vlastně již hotový; akorát bychom ještě měli spojit body A', B', C'.

Samodružný bod
V osové souměrnosti můžeme nalézt jeden speciální případ zobrazení. Jedná se o takzvanýsamodružný bod. Takovýto bod se v osové souměrnosti zobrazí sám na sebe, takže A=A'. Takovýto případ nastane pouze tehdy, leží-li bod A na ose o.

Osově souměrné útvary
Spousta různých geometrických těles má alespoň jednu osu souměrnosti. Rovnostranný trojúhelník má tři osy souměrnosti, rovnoramenný jednu. Vlastně se dá říci, že každý pravidelný mnohoúhelník má osu souměrnosti (má tolik os souměrnosti jako má vrcholů).

Těleso, které má nekonečně mnoho os souměrnosti je kruh, protože jakákoliv přímka vedená středem je osa souměrnosti. Osu souměrnosti můžeme nalézt i u prostorových útvarů (kužel, válec).
Nalezení osy souměrnosti
V předchozích příkladech jsme zobrazovali objekty osově souměrné podle osy o. Další typ příkladu, který můžeme dostat je nalezení osy souměrnosti, pokud známe původní i osově souměrný útvar. Nalezněte osu souměrnosti bodů A, A'.

Nejdříve musíme oba body spojit a najít střed S vzniknuvší úsečky AA'. Pokud nyní povedeme kolmici bodem S na úsečku AA', nalezneme osu souměrnosti:

Do kategorie shodných zobrazení patří i Středová souměrnost