Pokud jste četli předchozí články o stereometrii, neměli byste mít problém spočítat následující příklady.
První příklad
Máme pravidelný šestiboký hranol ABCDEFA'B'C'D'E'F'. Délka hrany |AB| = 4 cm a výškou v = 7 cm. Na tomto hranolu si ukážeme několik příkladů. Takto vypadá podstava:

Vypočítejte odchylku přímek AF a BC.
Na obrázku není vidět žádný průsečík těchto přímek, nicméně tento příklad je velmi jednoduchý.
My můžeme šestiúhelník rozdělit přímkou FC na dva stejné rovnoběžníky. Nás bude pochopitelně zajímat rovnoběžník ABCF. Když spočítáme úhly ∠AFC a ∠BCF, které jsou stejné, můžeme dopočtem do 180 (součet vnitřních úhlů trojúhelníku je 180°) získat zbývající úhel, tedy úhel mezi přímkami AF a BC. Velikost vnitřního úhlu šestiúhelníku je 120° (podle vzorečku α=((n-2)*180)/n), takže velikost úhlu ∠AFC = ∠BCF je 60°.

Úhel, který tedy svírají přímky AF a BC je roven γ = 180-(60+60) = 60°.
Tohle byl lehký příklad. Nyní zkuste vypočítat vzdálenost bodu, který vznikl na průsečíku přímek AF, BC (na obrázku bod G) a přímky EF.

Abychom mohli spočítat velikost úsečky PG, musíme nejprve určit délku úsečky FG a úhel ∠GFP.
Před chvílí jsme určili, že trojúhelník CFG je rovnostranný a proto můžeme říci, že FG = CF. Velikost úsečky CF můžeme také vyjádřit jako CF = 2*ρ, kde ρ je poloměr kružnice opsané a ten umíme spočítat podle vzorce:
ρ=a/(2*sin((180-α)/2))
V tomto vzorci je a = |AB| = 4 cm a hodnotu vnitřního úhlu jsme již vypočítali: α = 120°, takže:
ρ=4/(2*sin(30)) ρ=4 |FG| = 2*ρ |FG| = 8
Ještě musíme spočítat velikost úhlu ∠GFP. Spočítat jeho velikost je vlastně velmi jednoduché: |∠GFP| = 180-α, takže |∠GFP| = 60.

Nyní, když známe velikost úsečky FG a velikost úhlu ∠GFP, není problém spočítat velkost PG.
|PG| = |FG| * sin(|∠GFP|) |PG| = 8*sin(60) |PG| = 6.928
Vypočítejte vzdálenost bodu P od bodu D'. Nyní už přestáváme být v podstavě, konečně tedy budeme muset zapojit trochu více prostorovou představivost. V zásadě ale na tomto příkladu není nic složitého.

V první části musíme zjistit délku úsečky DP. Tuto úsečku můžeme spočítat z trojúhelníku DEP. V tomto trojúhelníku musíme určit velikost úhlu ε, velikost úsečky EP a velikost úsečky ED. Velikost úhlu ε už známe, protože to je vnitřní úhel šestiúhelníku a proto ε = 120°. Velikost úsečky ED už také známe, |ED| = 4 cm, takže jediný problém by mohl být získat velikost úsečky EP.
Z předchozích výpočtů už známe velikost úseček GP a FG. Jelikož úhel ∠FPG je pravoúhlý, můžeme spočítat velikost úsečky FP pomocí Pythagorovi věty:
|FP|2 = |FG|2 - |PG|2 |FP|2 = 82 - 6.9282 |FP| ≈ √16 |FP| = 4 |EP| = |EF| + |FP| |EP| = 8
Nyní můžeme kosinovou větou spočítat velikost úsečky PD.
|PD|2 = |EP|2 + |ED|2 - 2*|ED|*|EP|*cos(ε) |PD|2 = 82+42-2*8*4*cos(120) |PD|2 = 112 |PD| = 10.58
Podstava svírá s boční stěnou pravý úhel a proto stačí použít Pythagorovu větu pro spočítání vzdálenosti bodu P a D':
|PD'|2 = |DD'|2 + |PD|2 |PD'|2 = 72 + 10.582 |PD'|2 = 160.9364 |PD'| = 12.68
Necháme tento hranol již na pokoji a pokročíme k dalšímu příkladu.
Druhý příklad
Nyní jsme dlouho počítali, takže přijde na řadu rýsování. Do krychle o délce hrany |AB| = 4 cm vepište těleso jehož vrcholy budou ve středu všech stěn krychle ABCDEFGH.
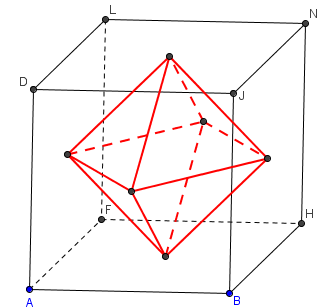
Vzniklé těleso je osmistěn, jedno z platónských tělese.
Vypočítejte objem a povrch osmistěnu.
Osmistěn můžeme rozdělit na dva stejné jehlany a spočítat objem a povrch jehlanu není problém. Stačí zjisti velikost výšky v a hrany a jehlanu. Výška je jasná. Je to polovina výšky krychle, tudíž v= 4/2 = 2. Vypočítat délku hrany a už je trochu těžší záležitost.

Pokud byste se na krychli podívali z jakékoliv strany, viděli byste toto. A určit velikost úsečky YZ umíme.
|YZ| = a = √(22+22 |YZ| = a = 2.82
Nyní již můžeme přikročit k samotnému výpočtu. Začneme objemem. Objem jehlanu spočítáme ze vzorečku Vj=1/3*a*a*v.
Vj=1/3*a*a*v Vj=1/3*2.82*2.82*2 Vj=5.301 cm3 Vosmistěnu = 2*Vj Vosmistěnu = 10.602 cm3
Plášť jehlanu v tomto případě tvoří 4 stejné trojúhelníky. V celém osmistěnu je těchto trojúhelníku 8. Stačí tedy spočítat povrch jednoho trojúhelníka a vynásobit výsledek osmi. Povrch trojúhelníku spočítáme podle vzorce St = (a*va)/2. Takže ještě musíme určit výšku.
va2 = 2.822 - 1.412 va = 2.44 St = (a*va)/2 St = (2.82*2.44)/2 St = 3.44 Sosmistěnu = St*8 Sosmistěnu = 27.52 cm2
Výsledný objem je 10.602 cm3 a výsledný povrch je 27.52 cm2.