Jak bylo řečeno v úvodu, středová souměrnost patří mezi shodná zobrazení. To znamená, že aplikováním středové souměrnosti se nemění vzdálenost bodů a velikost úhlů.
Pokud máme bod A a máme najít bod A2, který bude středově souměrný podle bodu S, povedeme přímku p body A, S. Bod A2 na této přímce leží a jeho vzdálenost je rovna vzdálenosti bodu A od bodu S. Jinými slovy musí platit toto:
Dost již ale bylo těch slovních definicí. Z příkladu vše pochopíte lépe. Máme bod A[2,2]. Nalezněte bod A' středově souměrný k bodu A podle bodu S[0,0].

Oba body musíme spojit přímkou p. Právě na této přímce bude ležet bod A'.
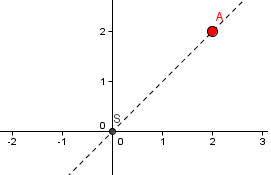
Víme, že |AS| = |A'S| a proto již lehce nalezneme bod A':

První příklad je za vámi. Přidám ještě několik dalších pro lepší pochopení. Narýsujte trojúhelník A'B'C', který bude středově souměrný podle bodu S[1,2] k trojúhelníku ABC, kde A[0,0], B[2,0], C[1,1].

Budeme postupovat úplně stejně jako v předchozím příkladě, akorát musíme stejnou proceduru opakovat postupně třikrát (pro body A, B, C).

Nyní stačí nalézt body A', B', C' na přímkách AS, BS, CS. Ale musíme dodržet podmínku |AS| = |A'S|, |BS| = |B'S|, |CS| = |C'S|.

Nalezení středu souměrnosti
Do teď jsme postupovali tak, že jsem měli zadaný bod S a nějaký útvar, který jsme zobrazovali. Může ale nastat opačná situace, tj. máme dva útvary a chceme určit střed souměrnosti. Určete střed souměrnosti bodů A[0,0], A'[2,2].

Střed souměrnosti nalezneme tak, že body A, A' povedeme přímku p. Pak určíme střed úsečky AA'. Střed je bodem S.

Jak již bylo řečeno, středová souměrnost patří mezi shodná zobrazení. Do této kategorie spadá také například osová souměrnost (přejít na článek Osová souměrnost).