V článku Funkce a jejich grafy jsem hovořil o dvou základních vlastnostech funkce - o definičním oboru a oboru hodnot. O těchto dvou prvcích už nebudu mluvit a přejdu rovnou k dalšímu bodu v plánu.
Rostoucí, klesající a prosté funkce
Základ je jednoduchý - rostoucí funkce je tam kde se zvyšuje její hodnota v oboru hodnot a klesající kde se její hodnota v oboru hodnot snižuje. Prostá funkce není omezená, tudíž se nedá říct, kde je rostoucí a kde klesající. Když není funkce prostá, je v určitém úseku (na ose x) rostoucí nebo klesající nebo někde rostoucí a někde klesající.
Rostoucí funkce:
- každé x náleží definičnímu oboru funkce
a
-
má v definičním oboru i v oboru hodnot nižší hodnotu než

Klesající funkce:
- každé x náleží definičnímu oboru funkce
a
-
má v definičním oboru nižší hodnotu než
, ale v oboru hodnot je tomu naopak

Z příkladu je patrné, že funkce je rostoucí i klesající. Klesající je v intervalu a rostoucí v intervalu
a tyto hodnoty jsou výsledky, kde je funkce klesající a kde rostoucí. Základním předpokladem rostoucích/klesajících funkcí je, že funkce není přímka (pak by byla funkcí prostou), ale že je v některém místě řekněme laicky zlomená nebo ohnutá a nebo také omezená (o omezenosti níže).
Prostá funkce:
- každé x náleží definičnímu oboru funkce
a
- mezi dvěma body na grafu a jejich hodnotami v definičním oboru a oboru hodnot není žádný vztah
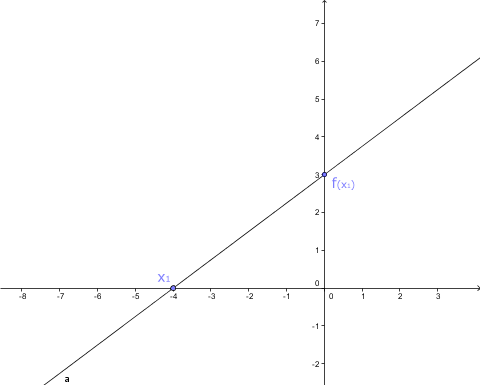
Sudost a lichost funkcí
Sudost a lichost funkce se určuje podle hodnoty určitého bodu v definičním oboru i oboru hodnot. Přejdu rovnou k věci.
Sudá funkce:
platí
- pro každé
v definičním oboru platí, že jeho záporná i kladná hodnota v definičním oboru má stejnou hodnotu v oboru hodnot => graf je osově souměrný podle osy y

Lichá funkce
platí
- pro každé
v definičním oboru platí, že jeho hodnota v definičním oboru je rovna hodnotě v oboru hodnot => graf je souměrný podle počátku

Omezenost funkcí
Omezenost se určuje podle hodnoty v oboru hodnot (podle hodnoty na ose y). Funkce může být omezená shora nebo zdola podle toho, jak je "otočená".
V grafech níže je funkce omezená zdola pětkou (nahoře) a funkce omezená shora čtyřkou (dole).


Doufám, že je smysl omezenosti z obrázků dobře patrný a není ho třeba dále rozvádět.
Minima a maxima
Určuje hodnotu z definičního oboru, kde je nabývá funkce nejnižší/nejvyšší hodnoty. Ale ne až tak úplně - lépe řečeno jsou to body, kde se funkce mění v rostoucí na klesající (pak je to maximum) nebo z klesající na rostoucí (pak je to minimum).

Tato funkce má minima v hodnotách -3, -1 , 1, 3 a maxima v hodnotách -2, 1, 2. Teď doufám, že je vše kolem vlastností funkcí jasné a těším se s vámi na příští část věnovanou lineárním funkcím.
